The content of this page is directly from B&H Photo

Large Format, Part 1
Large Format, Part 2

Introduction To Large Format, Part III

Contents:

Image Circle and Degree of Swing and Tilt 

The Scheimpflug Rule 

Close-Ups 

Yaw-Free 

Image Circle and Degree of Swing and Tilt

See 80k chart showing how Image Circle and Degree of Swing and Tilt works.
The circular image which a lens projects on the focal plane is called the "image circle." It is brightest in the center while (with a simple lens) both its quality and brightness deteriorate towards the edges. The image circle determines the lens usable field angle, one of the characteristics of every lens. The field angle is the angle between a line from the center of the lens to the outermost edge of the image circle, and a line to the center of the circle. This is a unique, fixed lens characteristic that has no relationship to focusing distance or image size. (It does, however, change with the lens aperture.)

The lens minimum image circle is measured at a particular focusing distance, usually at infinity. When a nearby object is focused upon, the lens moves farther from the film plane and, naturally, the image circle grows. In simple cameras without swing or tilt, the image circle and the optical axis of the lens always coincide. That means the diagonal of the film frame can, theoretically, be as long as the diameter of the image circle. However, cameras are usually designed with a somewhat smaller film frame to compensate for the loss in brightness toward the edge of the image circle.

In a large format camera with swing and tilt capability, the optical axis of the lens only in rare cases intersects the film plane at its center. When a generous amount of swing and/or tilt is applied, part of the film frame may wander outside the image circle. This means that the maximum permissible swing/tilt is limited by the size of the image circle.

Although the size of the image circle can be enlarged by extending the bellows, using excessive swing or tilt will result in part of the frame being outside the image circle. To prevent this from happening, it is necessary to take into account the lens type, image circle diameter and field angle before setting the degree of swing or tilt. Even lenses of identical focal length will have different field angles and image circles if their internal composition differs; telephoto lenses, for example, have a narrower field angle than their focal length would suggest.

The Scheimpflug Rule 

How does the Scheimpflug Rule really work? Check out this illustration. In order to use camera movements properly, an understanding of the Scheimpflug rule is essential. This is the principle which enables us to form a focused image of the subject even if it is at an angle relative to the camera at wide open aperture.

If the subject is at an angle relative to the optical axis of the lens, we can sometimes bring the whole of it into focus by closing down the lens aperture and thus increasing the depth of field. The problem cannot always be corrected simply by stopping down, however (see picture on left). A host of related problems can crop up as well, caused by such things as too slow a shutter speed or stopping down the aperture too much (which will cause the picture quality to deteriorate). Such difficulties are frequent when we rely only on small f-stops to solve the problem.

If we use camera movements based on the Scheimpflug rule however, we can bring the whole of an angled subject into perfect focus without stopping down the aperture at all. The Scheimpflug rule states that it is possible to keep in focus all of the subject provided that the axis formed by its surface, the axis of the camera front and the axis of the camera back all meet in a single point. The Scheimpflug rule is a technique no photographer using camera movements can ignore.

Close-Ups

Large format cameras permit macro or close-up photography without adding supplementary bellows or extension tubes. Most view cameras can achieve anywhere from a 1:1 magnification with a 210mm lens, up to 4:1 ratio with a 90mm lens. Yet if additional magnification is needed, usually a supplementary bellows can be added or a shorter focal length lens can be used.

Film exposure with a view camera is the same as that of any other camera, except that the bellows extension (the distance from the center of the lens to the film) and reciprocity failure more often need consideration. As the bellows extension increases, the intensity of the light reaching the film decreases. The formula is as follows: 

(bellows length) x² divided by (focal length) x² = exposure factor.

Assume that the focal length is six inches (150mm), and the bellows extension is twelve inches. Therefore:

12 (squared) divided by 6 (squared) = 144 divided by 36 =4x.

The exposure factor is 4x (or two stops), so if the indicated exposure is 1/250 at f/8, use a corrected exposure of 1/60 at f/8, or 1/125 at f/5.6 or 1/250 at f/4. A simpler way to figure the needed correction is the 50 percent rule: For every 50 percent increase of bellows extension over focal length, increase exposure by one stop. 

The table below converts exposure factor into an exposure value for you.

Exposure Factor	4X	5.6X	8X	11X	16X
Exposure Value	2EV	2.5EV	3EV	3.5EV	4EV

Yaw-Free

Yaw is defined as the sideways tilting of a standard when swing is applied to the standard after it has been tilted. This results in standards which are not parallel in any axis. A yaw-prone camera requires multiple adjustments to maintain depth-of-field and focus when two or more adjustments are made to the same standard. A yaw-free design allows the photographer to tilt and swing a standard without having the second adjustment negate the benefits of the first.

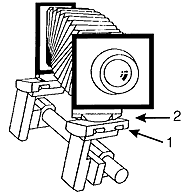
Whether a camera yaws or not depends on the sequence of the joints. If the joint for tilting about the horizontal axis (1) comes first in the standard block, the camera design is yaw-free.

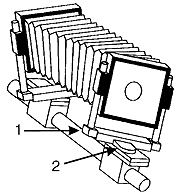
If however the joint for swinging round the vertical axis (2) is located ahead of the joint for tilting round the horizontal axis (1), the camera will be suject to yaw.